
The Effect of an Unusual Rain Event
In an email by an unmentioned person on 11/5/2012, the following statement was made: “There appears to be hydrological study/s which show that x amount of rain in the watershed would fill lake from tributary flow as well as rain fall accumulation on lake surface to point that it would threaten dam structure”
1. Introduction
I had several emails exchanges with the originator of that email, and other people that might be in the know, but was unable to locate the source of that statement nor the purported document.
This statement got me to thinking though: “What would be the height of the water flowing over the spillway during a very rainy period? Would the height of the flow go over the crest of the dam?”
2. Analysis
To determine this is a standard civil/mechanical engineering problem. I went about estimating this scenario in the following way.
The methodology for this problem is based on the weir equation (a weir is a barrier crossing a waterbody to alter the flow characteristics; the weir here being the concrete emergency spillway next to the dam). A brief derivation of a mathematical approximation is given here[^1] (one can include other factors, but this would make it unnecessarily complicated for the current purposes, which is to provide a ballpark estimate; for more exact solutions, see this US Corps of Engineers technical document[^2] and/or this Bureau of the Reclamation Engineering Monograph[^3].
Assume:
1. The grounds that make up the Deep Creek Lake watershed are totally saturated and all rainfall would flow directly into the lake or into the tributaries that feed the lake (NOTE: this is an absolute worst case, as if the whole watershed were covered by a plastic sheet that drains all water into the lake)
2. The lake’s watershed is 64.7 square miles.
3. The rain is falling uniformly(evenly) over the whole watershed.
4. The emergency spillway is approximately 720 ft long (as measured with Google Earth).
5. Use the basic mathematical equation (referenced above).
$$Q = \frac{2} {3} {C_d} L {\sqrt{2 g H^{\frac{3} {2} } } }$$
where:
Q = flow rate,
\(ft^3/sec\)
, rate of water flowing over the spillway
\(C_d\)
= coefficient of discharge (a function of the shape of the weir and the depth of the water in front of the weir; assumed to be 0.62, a common assumption)
L = length of the weir (spillway) (720 ft)
g = acceleration due to gravity (32.2 ft /
\(sec^2\)
)
H = the height (or depth) of the water sheet flowing over the weir.
Since H is what we’re looking for, this equation can be solved for H which takes on the following form:
$$H=\left[ {\frac{Q} {\frac{2} {3} C_d L \sqrt{2g}}} \right]^\frac{2} {3}$$
Q is calculated by the product of the rainfall rate and the area of the watershed. The question is what rainfall rate to assume? Again we will use a worst case assumption that the total annual rainfall falls within a single day (24 hrs).
The annual average rainfall is somewhere between 40 and 50 inches depending on the source. Assume the worst case, 50 inches in 24 hours. That translates into 24/50 = 0.48 inches per hour, say 0.5 inches per hour.
Figure 1 below shows the height of the water above the spillway., as calculated with the above formula. As can be seen, for the assumed 0.5 inches per hour, the height is approximately 6 ft.
Consider the following:
1. Elevation of the spillway: 2462.0 ft (Deep Creek Project drawings).
2. Elevation of the crest of the dam: 2475.0 ft (Deep Creek Project drawings)
Hence there is 13 ft from the top of the spillway to the crest of the dam. Given the 6 ft calculated above and the figure below for other conditions, this is not exceeded by a wide margin. Reviewing the basic assumptions:
1. All of the annual rain falling on the watershed happens in one day.
2. Completely saturated soil.
3. Raining uniformly all over the watershed.
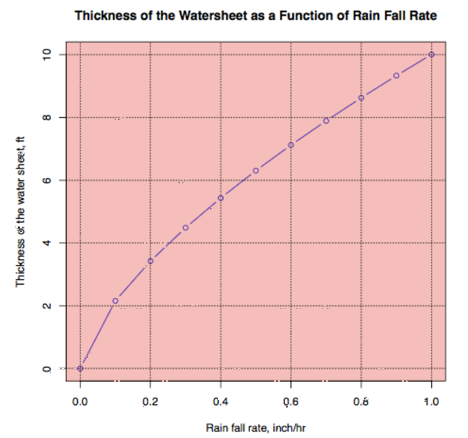
Figure 1. Thickness of the Water-sheet as a Function of Rain Fall Rate.
3. Conclusion
A highly unrealistic rain event will NOT cause the water from the lake to flow over the crest of the dam!
4. References
1. Weirs
2. Hydraulic Design Criteria
3. Discharge Coefficients For Irregular Overfall Spillways
PLV
First Published: 11/5/2012