
A Simple Recharge Model
Groundwater exfiltration into marine systems, is called, in the literature, submarine groundwater discharge (SGD) and is defined as “any and all flow of water on continental margins from the seabed to the coastal ocean, regardless of the fluid composition or driving force”.
Fresh water exfiltration into a lake is called lacustrine groundwater discharge (LGD) and includes any and all flow of groundwater from the lakebed to the lake.
These two parameters are difficult to quantify. The associated issues and an estimate of one form of SGD will be described here.
1. Introduction
The quantification of lacustrine groundwater discharge (LGD), as defined in Ref. 1, in water and nutrient balances of lakes is challenging and thus often neglected. References 2-13 address this issue, mostly for coastal areas. I shall not go in detail into the work performed by others, but the references at the end of this report form a starting point for a more exhausting modeling effort.
There are two types of recharge taking place at Deep Creek Lake, one caused by the sudden withdrawal of water by the turbines, and one, of longer duration and exhibiting a much slower recharge rate, by the very nature of groundwater flows. I’ll call these two recharge components as “Primary GroundWe shall consider the latter groundwater flow in Section 3. This type of groundwater flow is probably quite significant during and shortly after a period of rain. It’s existence is easiest seen in early winter when the lake begins to freeze. One can see all around the lake a region of open water resulting from the inflow of warm groundwater. The photo in Figure 1 demonstrates this effect.

Figure 1. Groundwater Discharge into the Lake.
2. The Secondary Recharge Model
The recharge by groundwater is very pronounced when the turbines cease to operate. We’ll look a small data set to get some approximation of the lake recharge rate.
Consider the data span shown in Figure 1. It’s the detailed lake level record starting June 2016, for 5 days. Also shown is when the generators are running. The data is not available whether one or both generators are running, but it will be assumed that both are, which is the normal mode of operation. One can observe some rise in the lake level after the generators shut down, but it’s not clear by how much because of the noise in the water level gage.
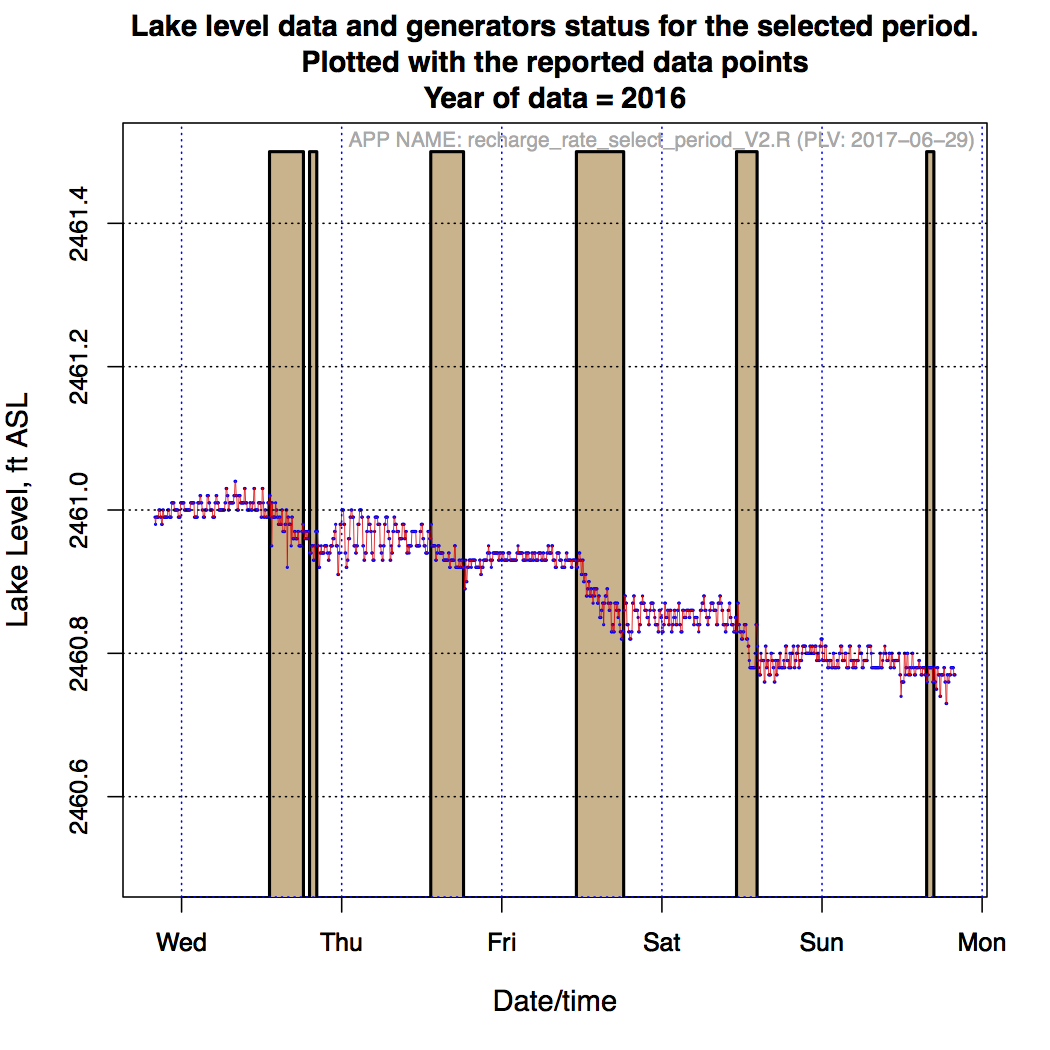
Figure 2. Lake Level and Generator Operation - raw data.
Figure 2 is passed through a Loess filter and smoothed with the span factor indicated, with the results shown in Figure 3. One can now see clearly the recharge after shutdown. The overall downslope of the curve suggests very little rainfall during this 5-day period.
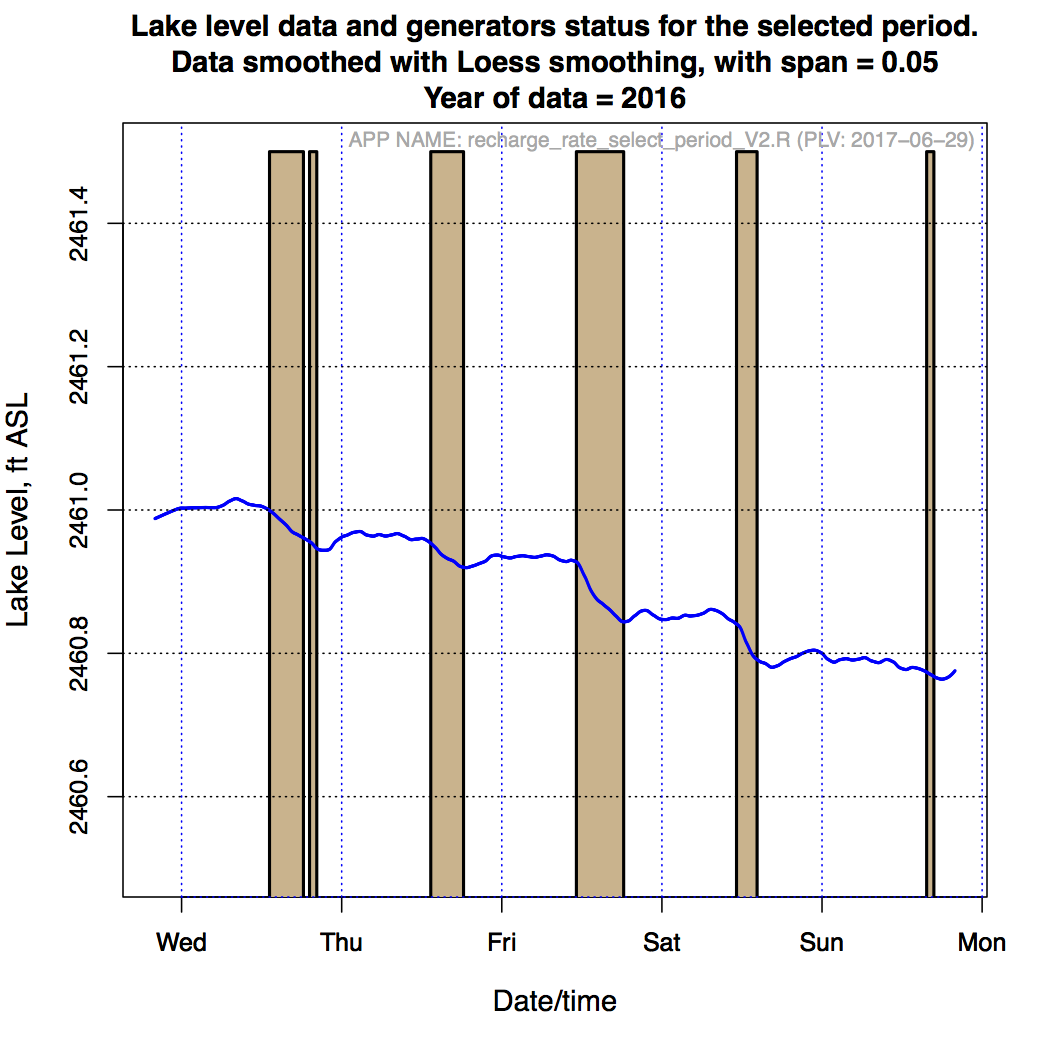
Figure 3. Lake Level and Generator Operation - smoothed data.
In Figure 4 we try to estimate the rate of recharge and the duration of recharge. Red straight line segments have been mated to the slopes of the recharge event and endpoints have been indicated by blue vertical lines.
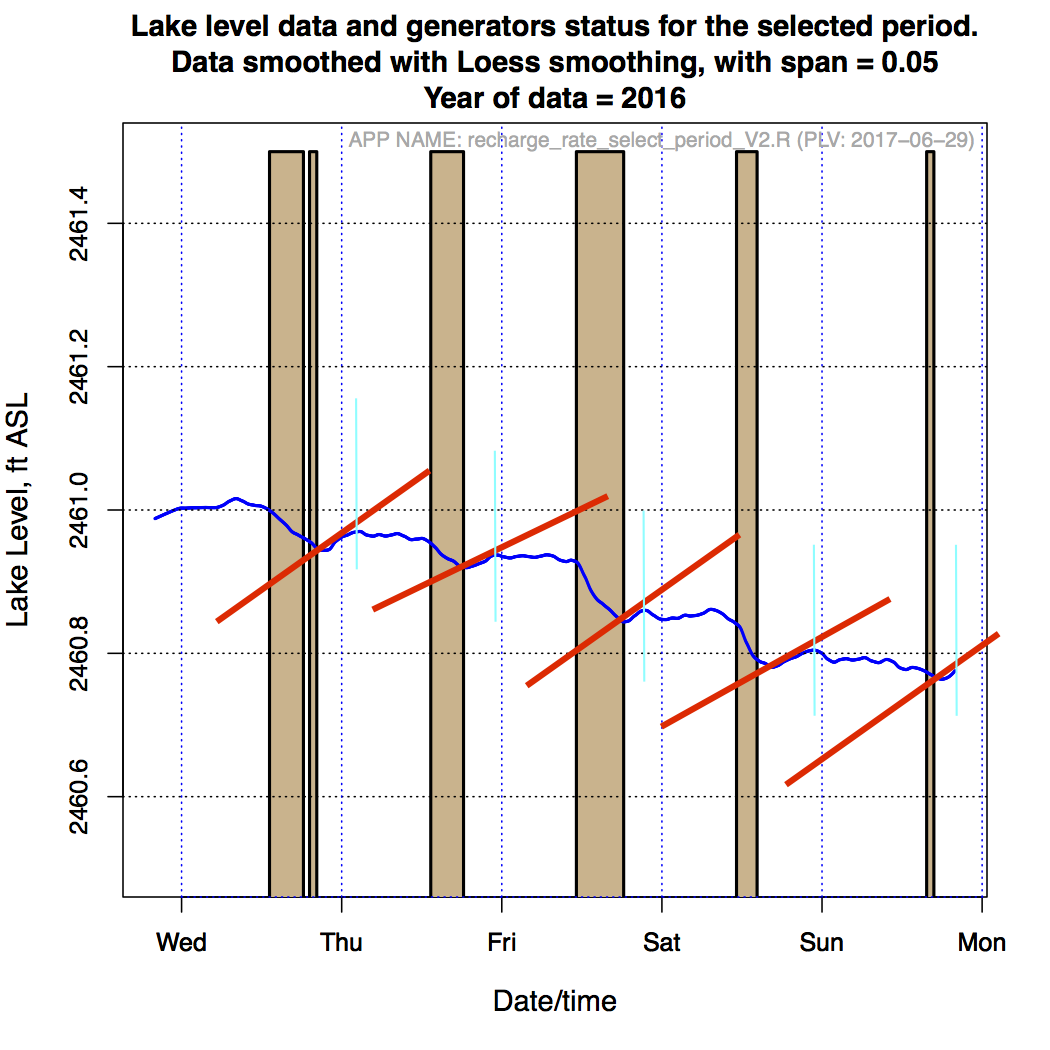
Figure 4. Lake Level and Generator Operation - recharge rate estimates.
A simple script was written evaluating the on-screen pixel measurements and the resulting mean recharge rate is computed to be 0.0065 ft/hr or 0.08 inches/hr. As far as the duration of the recharge, Figure 4 can make a case for that this equivalent to the duration of the generators being on just prior to the recharge takeoff point.
So this defines the simple secondary groundwater recharge model after generator operation.
> # Lake recharge rate
> # recharge_rate.R
>
> # the following array are measured slopes of recharge rate in degrees
> rate <- c(35.4, 26.2, 35.8, 29.4, 35.5)
>
> # NOTE: for calibration purposes, 0.2 ft of change in lake elevation is 172 pixels
> # 24 hrs = 196 pixels. This defines a slope of 41.5 degrees
>
> slope <- 0.2/24 # ft/hr
>
> # Assume that recharge rates are proportional to slopes
>
> real.rate <- rate * (slope / 41.5)
>
> aver <- mean(real.rate) # ft/hr
> aver
[1] 0.006518072
>
3. Primary Recharge Model
This is a topic of a separate note.
4. Further Work Needed
This note describes a simple model that may only be of value for just a few number of hours of generator operation. Factors, such as prior rain intensity, or duration of a dry period may affect the simple model. Also, the recharge rate when turbines are not operating should be determined probably as a function of prior rain intensity and duration of prior dry days.
5. References
- “From submarine to lacustrine groundwater discharge,” JÖRG LEWANDOWSKI, KARIN MEINIKMANN, FRANZISKA PÖSCHKE, GUNNAR NÜTZMANN & DONALD O. ROSENBERRY
- submarine groundwater discharge
- Phosphorus and Water, USGS
- Phosphorus in a Ground-Water Contaminant Plume Discharging to Ashumet Pond, Cape Cod, Massachusetts, 1999
- Nutrients and toxic contaminants in shallow groundwater along Lake Simcoe urban shorelines
- ESTIMATION OF NATURAL GROUND WATER RECHARGE Amitha Kommadat
- “An Analysis Of Hydrogeology, Groundwater Discharge, And Nutrient Input To Clear Lake”, Dr. William W. Simpkins, Keri B. Drenner, and Sarah Bocchi
- “Phosphorus and Groundwater: Establishing Links Between Agricultural Use and Transport to Streams”, Joseph L Domagalski and Henry Johnson
- “An Introduction to Submarine Groundwater Discharge”, USGS
- “Submarine Groundwater Discharge: An Unseen Yet Potentially Important Coastal Phenomenon”, D. Reide Corbett, William C. Burnett, and Jeffrey P. Chanton
- “Groundwater - the disregarded component in lake water and nutrient budgets. Part 1: effects of groundwater on hydrology,” Donald O. Rosenberry, Jörg Lewandowski Karin Meinikmann and Gunnar Nützmann
- “Phosphorus in groundwater discharge – A potential source for lake eutrophication,” Karin Meinikmann, Michael Hupfer, Jörg Lewandowski
- “Lacustrine groundwater discharge: Combined determination of volumes and spatial patterns,” Karin Meinikmann, Jörg Lewandowski, Gunnar Nützmann
PLV
First Published: 11/10/2017
Scripts associated with this effort can be found here and here